Rechercher



Les Sons Périodiques

Vous êtes ici : Audio >Apprendre
English Version...

Les sons périodiques sont ceux avec lesquels on peut écrire une mélodie ( par opposition aux bruits et percussions).

Les sons sinusoïdaux : ils n'existent pas dans la nature mais ils permettent d'analyser les sons réels. En effet, tous les sons périodiques et les sons réels sont quasiment périodiques. Ils sont engendrés par la vibration d'un corps sonore : hanche, corde, colonne d'air etc., sont décomposables en une somme de sons sinusoïdaux.

FOURIER a démontré mathématiquement que toute oscillation périodique peut être décomposée en une somme d'oscillations sinusoïdales selon une règle appelée LOI DE FOURIER.

Son sinusoïdal simple (ex La 440 Hz du téléphone quand on décroche). Il se décrit mathématiquement ainsi :

X=Asin(2p f t)

Où X représente le mouvement d'un point du corps sonore ( un point sur une corde, le déplacement d'une molécule d'air), A représente l'amplitude du son, f la fréquence, et t le temps.

FOURIER démontrait donc qu'un phénomène périodique (un son) résultait toujours de la superposition d'une série de sinusoïdes simples dont les fréquences étaient un multiple de la fréquence de base.

Exemple : prenons le Do1 dont la fréquence est de 65 Hz, la série des fréquences harmoniques qui en résultent sera la suivante : 65, 130, 195, 260, ..., ... n fois 65

Et c'est la somme des sons résultant de ces fréquences qui va produire un son sinusoïdal complexe.

Sa fonction mathématique s'exprimera ainsi :

X=A1sin(2pf t)+ A2sin(2p2f t)+ A3sin(2p3f t)+ A4sin(2p4f t))+ ... Ainsi jusqu'à l'infini...

An peut avoir n'importe quelle valeur. On remarquera toutefois que le plus souvent, sa valeur décroît proportionnellement à n.

Cette fonction permet d'engendrer n'importe quel son périodique et les valeurs de A1............ An vont déterminer le timbre du son.

Remarque importante : les sons réels, c'est a dire ceux produits par de vrais instruments, ne respectent pas tout a fait cette loi et les premiers synthétiseurs qui suivaient strictement ce principe n'ont jamais satisfait une oreille musicale !

Quelques exemples

(Cliquez sur les images pour écouter les exemples)

Signal sinusoïdal pur

Signal en dents de scie, toute la série des harmoniques est utilisée (Violon).

Signal carré, seules les harmoniques impaires sont utilisées.

Son de violon synthétique C4 ou do3 à 262 Hz.

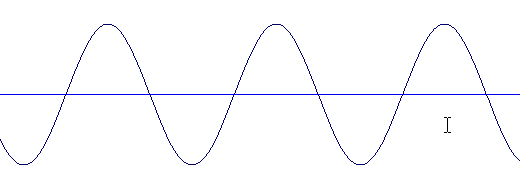
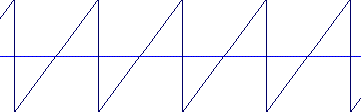
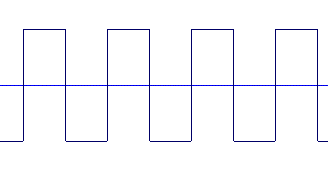
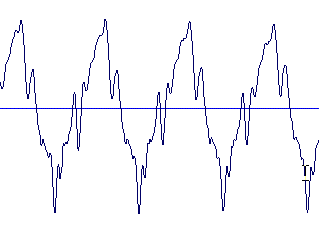
Remarquons déjà que le signal sinusoïdal semble moins défini en hauteur et que le signal carré semble plus aigu que le signal triangulaire.

Un excellent appareil permet de saisir le spectre harmonique d'un son et ainsi de se représenter par une image sa structure, c'est le sonagraphe.

Bruno CANADAS, le 05-04-2000
Page vue 30853 fois